在利用WPS对数据进行对称程度分析时,SKEW函数是经常使用到的重要工具。无论是判断数据是否对称分布,还是发现隐藏的极端值规律,SKEW函数都能提供关键线索。本文将带你全面了解SKEW函数,从核心概念到实战应用,让你快速掌握这一实用工具。
一、SKEW函数核心概念
(一)什么是SKEW函数?
SKEW函数全称为“偏态系数函数”,其核心作用是衡量数据分布的不对称程度。在WPS表格中,它通过计算一组数据与平均值的偏差,输出一个具体数值,直观反映数据分布的“偏斜度”——数值越偏离0,说明数据分布越不对称。
(二)为什么需要SKEW函数?
SKEW函数的价值在于提前发现数据的“分布特征”,为决策提供依据:
商业场景:某电商通过SKEW函数发现用户购买金额呈右偏分布(大部分用户消费低,少数用户消费高),据此推出普通用户小额促销、高消费用户专属权益的分层策略。
教育场景:老师用SKEW函数分析考试成绩,若结果为左偏(大部分学生分数高,少数分数低),可针对性辅导低分学生。
二、SKEW函数应用技巧
(一)语法结构:简单直接的公式模板
SKEW函数的语法为:SKEW(number1,[number2,…])
number1:必需参数,可输入数字、单元格区域(如A1:A10)或单元格引用;
[number2,…]:可选参数,最多支持255个,用于扩展数据范围。
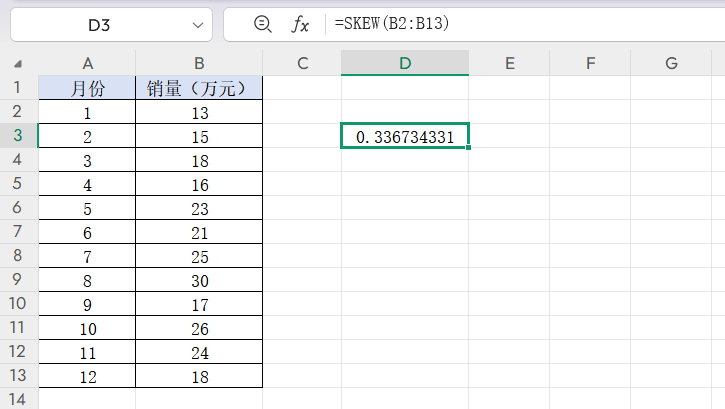
示例:计算B2到B13单元格的偏态系数,输入公式=SKEW(B2:B13),即可得到结果。
(二)参数注意事项:避免常见错误
数据类型:仅接受数值型数据,文本、逻辑值(TRUE/FALSE)、空白单元格会被自动忽略;若文本误存为数值格式(如“123”设为文本),需先修正格式。
数据范围:虽支持255个参数,但实际使用中建议引用连续区域(如A1:C100),更高效且不易出错。
(三)操作步骤:3步完成计算
- 准备数据:在WPS表格中录入需分析的数据(如员工工资、销售额);
- 插入函数:选中目标单元格,点击菜单栏“公式→统计→SKEW”,或直接输入“=SKEW(”;
- 设置参数:选择数据区域(如A1:C20),点击“确定”,结果自动生成。
三、SKEW函数结果解读
(一)结果对应的分布特征
- 值=0:数据呈对称分布,情况比较少见,可能比较常见与理想的数据模型;
- 值>0:右偏态分布,存在少数极大值拉高平均值(如居民收入,多数人收入中等,少数人收入极高);
- 值<0:左偏态分布,存在少数极小值拉低平均值(如难度过高的考试,多数人分数较高,少数人分数极低)。
(二)实例分析:从结果到结论
某店铺分析两组销售数据:
A组(普通工作日销售额):SKEW值接近0,说明每天销售额分布均匀;
B组(包含促销日销售额):SKEW值>0,因促销日的高额销售成为极端值,导致数据右偏。
四、SKEW函数实战场景:从数据到决策
1.市场调研:分析用户对某产品的满意度评分来进行产品优化策略;
2.财务分析:分析应收账款账龄等数据防范风险;
3.教育评估:分析学生作业完成时间,来实施精准教学
五、SKEW函数与其他函数的协同使用
1.搭配AVERAGE函数:反映数据的平均水平,SKEW函数反映分布形态,两者结合可避免被“平均值”误导:
2.结合IF函数:通过公式组合实现自动判断,例如:=IF(SKEW(A1:A10)>0,”存在高值极端数据”,”分布较均衡或存在低值极端数据”),该公式可自动标记数据偏态特征,适合批量数据的初步筛选。
六、使用SKEW函数的注意事项
样本量影响:样本量较小时(如少于30个数据),结果可能失真,建议使用100个以上数据提高准确性;
对比一致性:多组数据对比时,需保证统计标准一致(如比较不同班级成绩时,考试难度、评分规则需相同);
结合其他指标:SKEW值需配合平均值、中位数等指标分析,避免单一数据导致判断偏差。
结语
SKEW 函数就如同精准的罗盘,能量化数据的偏态程度,快速揭示数据偏离正态分布的情况,帮助我们捕捉数据趋势与异常。无论是市场调研分析,还是科研实验评估,SKEW 函数都是重要工具。






