在信息爆炸的当下，数据背后的波动规律往往比表面数值更有价值。无论是评估产品质量稳定性，还是分析团队绩效差异，都需要精准度量数据的离散程度——而总体标准差正是实现这一目标的核心工具。在WPS表格中，STDEV.P函数专为计算总体标准差设计。但是STDEV.P函数却常因与其他函数混淆、使用细节疏忽导致结果失真。本文将从零开始解析STDEV.P函数，助你真正用好这一数据洞察利器。
一、STDEV.P与STDEV的核心区别
二者适用场景界限严格。STDEV.P计算总体标准差，数据为完整研究对象，以数据个数（n）为自由度；STDEV计算样本标准差，数据是总体抽取的部分，以n-1为自由度。
比如分析一个班级45名学生成绩（该班级是研究总体），用STDEV.P；若班级是年级的抽样代表，则用STDEV。否则混淆使用函数可能导致结果存在显著偏差。
二、STDEV.P函数的使用方法
函数格式：STDEV.P(number1,[number2],…)
number1是必需参数，是首个总体数据，可输入数值或引用单元格区域；
[number2],…是可选参数，最多254个。
示例：直接输入数值用STDEV.P(20,22,19,21,23)；
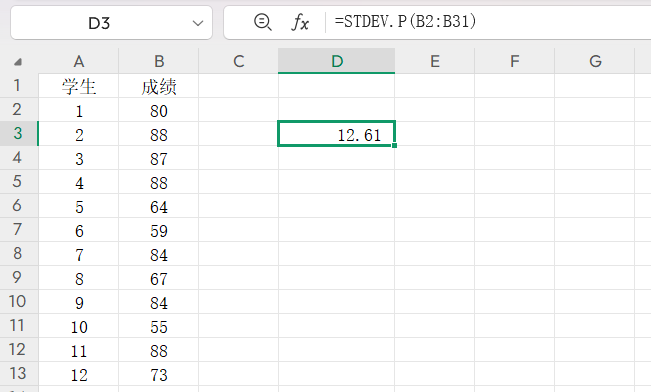
引用单元格用STDEV.P(B2:B31）。（计算B2到B31的总体标准差）
注意：引用区域需排除无关数据，避免结果失真。
三、STDEV.P函数的应用场景
- 教育领域：评估成绩稳定性。一班平均分82、标准差6.3，二班平均分80、标准差11.2，可见一班成绩更集中。
- 生产管理：监控产品质量。某批次电容检测，用STDEV.P算出标准差0.08μF，在≤0.1μF的标准内，生产稳定。
- 企业运营：分析绩效稳定性。销售团队月度成交金额，上月标准差9.8，本月7.2，业绩差异缩小。
- 金融投资：度量收益风险。某投资者持有的基金，用函数算出标准差4.3%，标准差小则收益波动平缓。
四、使用时的常见错误及解决办法
- 混淆总体与样本选错函数：明确研究范围，数据覆盖全部研究对象用STDEV.P。
- 数据混入非数值内容：提前清洗数据，将文本转对应数值；检查格式，统一文本型数字格式。
- 数据量不足致错误：确保至少有2个有效数值，单个数据无需计算。
五、函数组合使用
- 与AVERAGE搭配，能同时了解数据集中趋势和离散程度。
- 与MAX、MIN组合，可分析波动范围和离散程度。
- 与IF联动，能计算特定条件下的总体标准差。
结语
STDEV.P函数的价值，在于将抽象的“数据波动”转化为可量化的数值，让隐藏的规律浮出水面。无论是教师分析成绩、工程师监控质量，还是管理者评估绩效，只要牢记“总体数据用STDEV.P”的核心原则，避开数据格式、样本类型等常见陷阱，就能让这一工具成为数据决策的“透视镜”——不仅看到数据的表面数值，更能洞察其背后的离散规律。
iOS
Android
Windows
macOS